Приняв уравнение Лоренца, зададим себе несколько вопросов. Первый: что представляет собой k?

Чтобы ответить на этот вопрос, рассмотрим какое-либо тело, имеющее массу, покоящимся относительно наблюдателя. В этом случае его скорость равна нулю, и поскольку 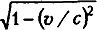v = 0, тогда v/c = 0 и (v/c)² = 0. Более того,  тогда превращается в , или , или 1.

Это означает, что для какого-либо тела, покоящегося относительно наблюдателя, уравнение Лоренца приобретает вид m = k/1 = k. Из этого мы можем заключить, что k — это масса тела в покое относительно наблюдателя. Ее обычно называют массой покоя и обозначают m₀. Уравнение Лоренца записывают следующим образом:

Следующий вопрос: что произойдет, если объект движется со скоростью большей, чем самая высокая скорость, представленная выше в таблице. Предположим, что объект движется со скоростью 1,0с относительно наблюдателя; другими словами, он движется со скоростью света.

В этом случае выражение под корнем уравнения Лоренца выглядит так:

Это означает, что для тела, движущегося со скоростью света, уравнение Лоренца приобретает вид: m = m₀/0, а из основ математики мы знаем, что делить на ноль нельзя. Математически уравнение Лоренца становится бессмысленным для тела, имеющего массу и движущегося со скоростью света.

Хорошо, тогда давайте возьмем другую скорость.

Пусть скорость из уравнения 2 будет больше 0,9с — при этом выражение под корнем начнет быстро приближаться к нулю, а значение m — стремительно возрастать. Это происходит независимо от значения m₀. (Постарайтесь сами рассчитать m для значений скорости 0,99, 0,999 и 0,9999 и так далее, насколько у вас хватит терпения.)

На языке математики мы можем сказать, что в уравнении с = а/b (где а больше, чем 0) при приближении b к нулю с увеличивается беспредельно, то есть это можно записать так: а/0 = ?, где ? представляет собой неограниченное возрастание, или бесконечность.

Тогда мы можем сказать, что для любого объекта, имеющего массу (какой бы малой она ни была), эта масса приобретает бесконечные значения, когда его скорость приближается к скорости света относительно наблюдателя.

Это означает, что тело не может в действительности достичь скорости света (хотя оно может бесконечно стремиться к этому значению) и определенно не может ее превзойти. Вы можете аргументировать это следующим образом.

Единственный известный нам метод заставить какой-либо объект двигаться с большей величиной, чем скорость света, — это приложить к нему силу, которая бы произвела это ускорение (см. главу 6). Однако чем больше масса, тем меньше ускорение, произведенное данной силой, и, таким образом, когда масса приближается к бесконечным величинам, ускорение, каким бы большим поначалу оно ни было, будет стремиться к нулю. Следовательно, ни один объект не может двигаться быстрее, чем скорость, при которой масса становится бесконечной.

Второй аргумент таков. Движущееся тело имеет кинетическую энергию, которую мы можем считать равной mv²/2, где m — масса, a v — скорость. Если к телу прикладывается сила таким образом, что кинетическая энергия возрастает, эта энергия может увеличиться потому, что увеличивается v, или потому, что увеличивается m, или же из-за одновременного увеличения как v, так и m. При обычных скоростях все изменения происходят только со скоростью, так что мы можем предположить (хотя это предположение неверное), что масса остается постоянной при всех обстоятельствах.

Однако на самом деле как скорость, так и масса возрастают в результате приложения силы, но изменение массы столь незначительно при обычных скоростях, что измерения незаметны. Однако когда скорость относительно наблюдателя возрастает, то все больше энергии будет затрачиваться на увеличение массы и меньше — на возрастание скорости. Ко времени, когда скорость окажется очень близкой к скорости света, фактически вся энергия будет затрачиваться на увеличение массы, и ничего не будет оставаться на увеличение скорости. Это приведет к тому, что скорость света никогда не будет достигнута.

И не спрашивайте почему. Так устроен мир.

Однако я надеюсь, вы заметили, что, рассказывая о бесконечном возрастании массы при скорости света, я был вынужден утверждать: «Это правда независимо от значения m₀ — важно лишь то, что оно отлично от нуля».

Конечно, все частицы, из которых мы состоим, — протоны, электроны, нейтроны, мезоны, гипероны и так далее, — имеют массу покоя больше нуля, так что эта оговорка не кажется очень ограничивающей. В самом деле, люди обычно говорят: «Невозможно достичь или превысить скорость света», не уточняя, что они имеют в виду объекты, имеющие массу покоя большую, чем ноль, поскольку они считают, что такими являются все объекты.

Я не уточнял это в статье «Невозможно, и это все», что и дало возможность посчитать меня занудой. Если мы примем во внимание это ограничение, тогда все, что я сказал, примет законченный вид.