Еще мы с матерью пошли в магазин и купили книгу, которая называется «Высшая математика для степени А», и отец сказал миссис Гаскойн, что я буду сдавать экзамен на будущий год, и она ответила:
— Ладно.
Так что я собираюсь сдать экзамен по высшей математике и получить степень А. А через два года я сдам экзамен по физике и тоже получу степень А.
И когда я это сделаю, то поеду в другой город и поступлю в университет. И это будет не в Лондоне, потому что мне не нравится Лондон, а университеты есть во многих местах, и не обязательно в больших городах. Я буду жить в доме с садом и собственным туалетом и заберу туда Сэнди, свои книги и свой компьютер.
И потом я получу Почетную Степень Первого Класса и стану ученым.
Я знаю, что смогу это сделать, потому что я сумел самостоятельно съездить в Лондон и потому что я сумел выяснить, кто убил Веллингтона. Еще я нашел свою мать, я был смелым, я написал книгу, и это значит, что я могу все.
ПРИЛОЖЕНИЕ
Вопрос
Докажите, что:
треугольник со сторонами, которые могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1) является прямоугольным.
Докажите, что обратное утверждение неверно.
Ответ
Сперва мы должны определить, какова самая длинная сторона треугольника со сторонами, которые выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1).
n2 + 1 — 2n = (n — 1)2.
Если n > 1, то (n — 1)2 > 0.
Следовательно, n2+1 — 2n > 0.
Следовательно, n2 + 1 > 2n.
Сходным образом (n2 +1) — (n2 — 1) = 2.
Следовательно, n2 + 1 > n2 — 1.
Это значит, что n2 + 1 является самой длинной из сторон треугольника со сторонами, которые могут быть выражены формулой n2 + 1, n2 — 1 и 2n (где n > 1).
Для наглядности можно показать это на следующем графике (хотя это ничего не доказывает):
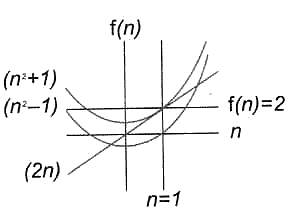
Согласно теореме Пифагора, если сумма квадратов катетов (двух более коротких сторон) равна квадрату гипотенузы (длинной стороны), треугольник является прямоугольным. Следовательно, чтобы доказать, что треугольник прямоугольный, нам нужно показать, что это тот самый случай.
Сумма квадратов двух более коротких сторон равна (n2 — 1)2 + (2n)2.
(n2 — 1)2 + (2n)2 = n4 — 2n2 + 1 + 4n2 =
Квадрат гипотенузы равен (n2 +1)2.
(n2 + 1)2 =
Таким образом, сумма квадратов коротких сторон равна квадрату длинной стороны. Следовательно, треугольник является прямоугольным.
А утверждение, обратное утверждению: «Треугольник со сторонами, которые могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n >1) прямоугольный», — это: «Прямоугольный треугольник имеет стороны, которые могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1)».
И это значит, что нужно найти треугольник, который будет прямоугольным, но стороны которого не могут быть выражены формулами n2 + 1, n2 — 1 и 2n (где n > 1).
Итак, пусть гипотенуза прямоугольного треугольника АВС будет АВ.
Пусть АВ = 65.
Пусть ВС = 60.
Тогда

Пусть АВ = n2 +1 = 65.
Тогда


